Es la vida pasajera
Y todos pelan el diente,
Aquí está la calavera,
Del que ha sido presidente.
También la de Don Ramón
Y todos sus subalternos
Son como Buenos Gobiernos
Calaveras del montón
Es mi internet y busco como quiero
Casi seguro que has utilizado algún buscador de internet alguna vez. Es incluso posible que hayas llegado a esta página a través de uno de ellos. Y muy posiblemente, el buscador elegido para la tarea haya sido Google.
¿Te has preguntado alguna vez cómo funciona Google? ¿Cómo posiciona las páginas para mostrarlas antes o después en una lista de resultados de búsqueda? No, no es magia, lo que hay detrás de todo eso son matemáticas.
Pues en esta entrada vamos a construir un buscador en una internet de mentira. Pasen y vean.
View original post 2,500 more words
Compártelo
Sobre el origen de la maldad
La maldad es un tema recurrente en la filosofía, la psicología y la religión. A menudo éstas se preguntan sobre su origen. El punto de vista religioso nos dice en el génesis que la maldad surge de la inminente desconexión entre el micro y el macrocosmos (el ser humano y la divinidad, respectivamente) producto de la expulsión del hombre del paraíso.
Entre otros intentos de explicar el origen del mal, está, por ejemplo, la Paradoja de Epicuro, que concluye (basándose en premisas y la lógica proposicional convencional) que la existencia de una deidad con ciertas características y la existencia del mal son mutuamente excluyentes.
El el campo de la psicología encontramos otras respuestas: el mal se origina por la constante fijación de expectativas de el ser humano hacia el mundo que le rodea, el mal es un placer mal dirigido, el mal es en esencia, relativo.
No hay respuesta clara sobre el origen del problema, ni la habrá. Mas un punto de vista muy interesante, el que he querido resaltar en esta breve ocasión (y quizás el más acertado o el más engañoso) es el que sugiere la imagen siguiente:
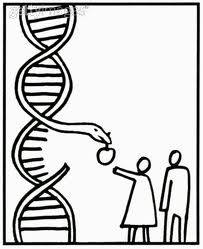
A simple vista, parece que se reproduce una escena representativa de la biblia, que automáticamente asociamos con el génesis: el momento es que Eva come del fruto prohibido (el fruto del conocimiento) por influencia de la serpiente y luego Adán por influencia de su compañera.
Sin embargo algo llama la atención: ¿Que hay de las cadenas de ADN? ¿Qué hace la serpiente, saliendo del ADN?
De acá se pueden sacar una importante conclusión: el mal es un atributo inherente en el ser humano. El mal, si existe, es parte de nuestra naturaleza humana.
Esta visión puede ser un poco determinista, vaga y poco pragmática. Sucede que no es mi intención hacer un análisis profundo sobre el problema del mal, mas no he podido dejar de maravillarme por la sencillez de esta imagen y las muchas ideas que sugiere.
Compártelo
25 películas para despertar nuestra conciencia política
Solemos asociar la política con dos extremos: un performance público ridículo y de mal gusto o una oficina a puertas cerradas en donde turbios personajes deciden en su beneficio el destino del resto de los mortales. El cine, en algunos curiosos casos, ha sido capaz de interpretar de manera lúcida ambas manifestaciones. De hecho, es quizás el medio artístico que mejor lo ha logrado.
El abordaje audiovisual frontal de temas políticos ha florecido especialmente en el género documental. Sin embargo importantes directores de cine, entre ellos algunos de sus principales genios como Orson Welles, Glauber Rocha, Stanley Kubrick y Charles Chaplin, han intentado proyectar la luz del Séptimo Arte en la frecuentemente oscura habitación de la política. El resultado ha ido desde la burda propaganda ideológica hasta obras de extraordinario poder para generar cambios de conciencia.
En una famosa escena de la película The Matrix, el protagonista tiene la…
View original post 1,327 more words
Compártelo
Un poema de Hugo Lindo
Cuando digo “te amo”,
yo pronuncio palabras radicalmente nuevas.
Nunca nadie
vertió en ellas el tono cabal,
el mismo arrobo.
Ni yo mismo dos veces.
Cada ocasión es otro reflejo de otras aguas.
No puede repetirse
Sino aquello que es repetible. Y esto
se niega a persistir, danza, se muda,
se convierte en amor de mil maneras.
Ni el sonido es el mismo: las palabras
se acortan,
se tropiezan,
se entrecruzan
en una fuga alucinante y múltiple.
Una vez, por ejemplo,
un niño triste se asomó a mis labios
y cayó en tus oídos
como una flor herida por mitad del aroma.
Otra vez, en las sílabas menudas
estaban todo el mar,
todo el olvido,
todas las dimensiones del naufragio.
Tuviste miedo entonces.
Miedo de las figuras ya borrosas,
de los fantasmas ávidos de un beso,
de las tormentas
apaciguadas hoy bajo la espuma.
Cada minuto es nuevo.
Cada voz, otra voz.
y cada frase un sueño inaugurado,
una aurora distinta, una ventana,
una estrella que brota de repente,
una camelia virgen,
una luna,
una manera intacta de quererte.
Si algún día dijiste
“ya he tenido esta rosa en mi regazo”,
no logró la verdad sitio preciso
en tu deseo de afirmar las cosas.
Porque esta rosa es nueva.
Es otra rosa.
Es una que amanece,
que parece,
que vuelve a madrugar dentro del pecho,
siempre distinta y de fugaz aroma.
Nunca la viste ayer, ni podrás verla
en instantes futuros.
Se sucede
como las lluvias del invierno.
Cae
siempre que te susurro estas palabras
radicalmente nuevas,
nunca dichas,
por nadie,
ni siquiera por mí, que las pronuncio.
Compártelo
DIÁLOGO EN LA TINIEBLA.
No busco la verdad, pero persigo
su estela cautivante, su aleteo
que es la réplica infiel de lo que creo
y el huidizo fulgor de lo que digo.
La verdad absoluta es un castigo
que quizás no merezca mi deseo.
Y su ausencia es el último trofeo
que desvela mi angustia de testigo.
Me quedo con la flor de la pregunta,
aspirando el aroma sin respuesta,
dejando que el silencio apenas hable.
Y al sentir que la lágrima despunta,
la verdad, como un grillo, me contesta
desde el jardín del vértigo insondable.
David Escobar Galindo
Compártelo
Explorando los números complejos: El conjunto de Mandelbrot
“El verdadero SER de la matemática radica en su capacidad inagotable de formular problemas, pero a diferencia de otras ciencias, no sólo se contenta en hallar sus soluciones, sino que, para resolverlos puede crear teorías, que a su vez generan nueva matemática. Ésta es precisamente la esencia de su dinamismo creador”
– Enzo R. Gentile
La base de los números complejos es el número imaginario, mejor conocido como i. Históricamente, este número fueron estudiados por matemáticos como Gauss y Euler. Surgieron de la solución de la siguiente expresión:
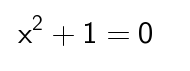
El número se representa con la letra i (de imaginario) ya que no existe número real tal que al multiplicarse por sí mismo, el resultado sea negativo. Ahora bien, ¿Qué es un número complejo? un número complejo es todo número de la forma:
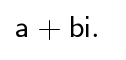
Tanto a como b, pertenecen al conjunto de los números reales, de manera que un número complejo tiene una forma real y otra imaginaria. Al introducir la unidad conocida como número imaginario, nótese que se ha creado un nuevo conjunto numérico: Los números complejos.
Como es de suponer, este nuevo conjunto tiene sus particularidades y asuntos interesantes sobre los cuales pueden surgir cosas increíbles, por ejemplo:
Supongamos que tenemos un número Z que pertenece al conjunto de los números complejos. Se tiene también la siguiente función iterativa:
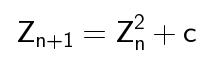
En la que tomamos el número Z, lo elevamos al cuadrado y añadimos una constante, al resultado le aplicamos la misma operación y así sucesivamente. Hasta acá tenemos dos posibilidades que conciernen a la constante C:
Para este estudio, se considerará nada más la posibilidad en la que el número inicial Z y la constante son iguales. Entonces, si tomamos un número complejo y le aplicamos esta operación y graficamos en el plano complejo (plano de coordenadas rectangulares con eje x real y eje y imaginario) cada punto resultante de la función y los unimos con segmentos de rectas, ¿Qué sucede?
Sucede lo siguiente:
Para algunos valores de Z, la función iterativa crece sin cota, podría decirse que escapa hacia el infinito.
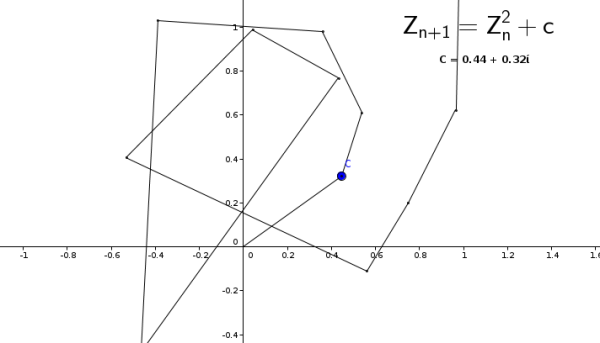
Mientras que para otros valores iniciales de Z, la función “no escapa” o está acotada.
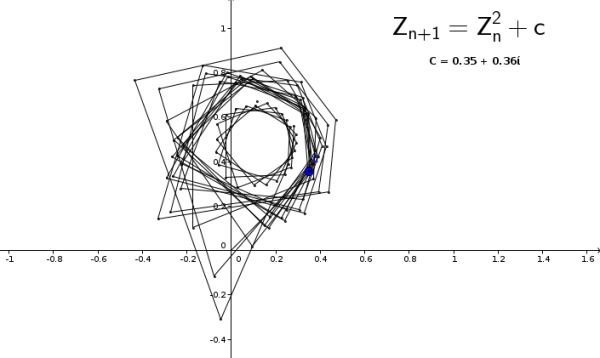
Los que no escapan, son los puntos que nos interesan. Por ejemplo, se muestran a continuación las trayectorias de distintos valores de Z que no escapan:
Ahora bien, ¿Qué pasa si graficamos punto por punto todo el conjunto de números complejos, tales que al aplicarles la función iterativa, estos estén acotados?
Sucede lo siguiente:
Se genera un fractal llamado Conjunto de Mandelbrot, en honor al matemático Benoît Mandelbrot (1924-2010). Precursor y creador de la geometría fractal.
Algunas definiciones del Conjunto de Mandelbrot son:
“El conjunto de todos los números tales que la función Z=Z²+C, Con un valor inicial Z=0, no escapa al infinito o esta acotado”
“El conjunto de todos los números complejos tales que el Conjunto de Julia asociado a esos puntos es un conjunto conexo”
Luego de leer las definiciones, podríamos estar familiarizados con la primera, pero ¿Que hay de la segunda?, ¿Que es un conjunto de Julia?, ¿Qué es un conjunto conexo?
Sucede que para cada punto del plano complejo, existe un conjunto llamado Conjunto de Julia asociado a dicho punto. Estos conjuntos surgen de aplicar el mismo polinomio cuadrático complejo pero esta vez el parámetro C y el valor inicial Z, son diferentes. Entonces el conjunto de Mandelbrot es el conjunto de todos los números tales que a cada número del conjunto M, le corresponde un conjunto J que es conexo, en otras palabras, está formado de una sola pieza.
Se ahondará más sobre ello en las próximas entradas sobre números complejos:
Explorando los números complejos: Conjuntos de Julia
Explorando los números complejos: Generar conjunto de Mandelbrot en GeoGebra.
Referencias:
Herren, Gustavo. Fractales: Las estructuras aleatorias. Compendios, 2002. ISBN: 987-550-061-5
Bibliografía recomendada:
Steward, Ian. Les fractals. Colección Les chroniques de Rose Polymath, Librairie Classique Eugene Berlin, 1982
Blanchard, P. Complex analytic Dynamics on the Riemann sphere. En Bulletin (new series) of the American Mathematical Society.
Lesmoir-Gordon, Niguel; Rood, Will y Edney, Ralph. Introducing Fractal Geometry. Icon book UK, 2000
Peitgen, Heinz-Otto y Jurgens, H. Fraktale, Gezahmtes Chaos. Carl Stiftung Fiedrich von Siemens, 1988.
Chaos and Fractals: Proceedings of Symposia in Applied Mathematics. Vol 39, American Mathematical Society.
Enlaces útiles:
Generadores de fractales en línea:
1-http://www.easyfractalgenerator.com/mandelbrot-set-generator.aspx
2-http://arquimedes.matem.unam.mx/PUEMAC/PUEMAC_2008/fractales/html/index.html
3-http://www.fractalposter.com/fractal_generator.php
Software utilizado
GeoGebra versión 4.0.10.0 Debian package. Sitio web: http://www.geogebra.org/
Fraqtive 0.4.5. A Mandelbrot family fractal generator. Licensed under the GNU General Public License. Sitio web: http://fraqtive.mimec.org
Compártelo
Tres libros de Jorge Luis Borges
¿En busca de una nueva lectura? ¿Por qué no leer un maravilloso libro de Jorge Luis Borges? Clic en la imagen para descargar.
1. El libro de los sueños:
“Pao Yu soñó que estaba en un jardín idéntico al de su casa. ¿Será posible, dijo, que haya un jardín idéntico al mío? Se le acercaron unas doncellas. Pao Yu se dijo atónito: ¿Alguien tendrá doncellas iguales a Hsi-Yen, a Pin-Erh y a todas las de casa? Una de las doncellas exclamó: “Ahí está Pao Yu. ¿Cómo habrá llegado hasta aquí?” Pao Yu pensó que lo habían reconocido. Se adelantó y les dijo: “Estaba caminando; por casualidad llegué hasta aquí. Caminemos un poco”. Las doncellas se rieron. “¡Qué desatino! Te confundimos con Pao Yu, nuestro amo, pero no eres tan gallardo como él.” Eran doncellas de otro Pao Yu. “Queridas hermanas”, les dijo, “yo soy Pao Yu. ¿Quién es vuestro amo?” “Es Pao Yu”, contestaron. “Sus padres le dieron ese nombre, compuesto por los dos caracteres Pao (precioso) y Yu (jade), para que su vida fuera larga y feliz. ¿Quién eres tú para usurpar su nombre?” Y se fueron, riéndose.
Pao Yu quedó abatido. “Nunca me han tratado tan mal. ¿Por qué me aborrecerán estas doncellas? ¿Habrá, de veras, otro Pao Yu? Tengo que averiguarlo.” Trabajado por estos pensamientos, llegó a un patio que le resultó familiar. Subió la escalera y entró en su cuarto. Vio a un joven acostado; al lado de la cama reían y hacían labores unas muchachas. El joven suspiraba. Una de las doncellas le dijo: “¿Qué sueñas, Pao Yu? ¿Estás afligido?” “Tuve un sueño muy raro. Soñé que estaba en un jardín y que ustedes no me reconocían y me dejaban solo. Las seguí hasta la casa y me encontré con otro Pao Yu durmiendo en mi cama.” Al oír el diálogo Pao Yu no pudo contenerse y exclamó: “Vine en busca de un Pao Yu; eres tú”. El joven se levantó y lo abrazó, gritando: “No era un sueño: tú eres Pao Yu”. Una voz llamó desde el jardín: “¡Pao Yu!” Los dos Pao Yu temblaron. El soñado se fue; el otro decía: “¡Vuelve pronto, Pao Yu!” Pao Yu se despertó. Su doncella Hsi-Yen le preguntó: “¿Qué soñabas, Pao Yu? ¿Estás afligido?” “Tuve un sueño muy raro. Soñé que estaba en un jardín y que ustedes no me reconocían…”.”
2. Borges and Mathematics.
“…as soon as I began to review his complete works in a methodical, “mathematical” way, Borges’ lifelong, enduring fascination and curiosity about that discipline emerged in all their lucidity: his pride in those aspects he had mastered, the little lessons he presented in some of his essays, the reviews, and readings of mathematical books. Suffice it to say that I was able to find almost 200 citations with mathematical allusions throughout his oeuvre, and a bibliography of 45 mathematical works consulted or cited.1 Beyond this rather impressive body of references, most interesting and revealing for me was the discovery of clear traces of some mathematical ideas behind several of his fictions, and an awareness of the subtle way in which mathematical concepts were transmuted and imbued with new life within a context of literary intentions. To study Borges’ appropriation of these ideas and to analyze them within each fictional work without separating them from those literary intentions, with the facets and layers of meaning they add, is the fundamental purpose of this book.”
3. Libro del cielo y del infierno
“Este libro es la reencarnación de otro más extenso,, más lento y acaso menos exigente que hace años compilamos: algo de resignada biblioteca o de archivo impersonal había en él: cada uno de los diversos libros sagrados que la humanidad ha compuesto nos, había legado una considerable cuota de páginas; felizmente aquella obra nunca se publicó.
El criterio que hoy nos guía es distinto. Hemos bus cado lo esencial, sin descuidar lo vivido, lo onírico y lo paradójico. Tal vez nuestro volumen deje entrever la milenaria evolución de los conceptos de cielo y de infierno; a partir de Swedenborg se piensa en estados del alma y no en un. establecimiento de premios y otro de penas.”
Compártelo
La noche cíclica
A Silvina Bullrich
Lo supieron los arduos alumnos de Pitágoras:
Los astros y los hombres vuelven cíclicamente;
Los átomos fatales repetirán la urgente
Afrodita de oro, los tebanos, las ágoras.
En edades futuras oprimirá el centauro
Con el casco solípedo el pecho del lapita;
Cuando Roma sea polvo, gemirá en la infinita
Noche de su palacio fétido el minotauro.
Volverá toda noche de insomnio: minuciosa.
La mano que esto escribe renacerá del mismo
Vientre. Férreos ejércitos construirán el abismo.
(David Hume de Edimburgo dijo la misma cosa.)
No sé si volveremos en un ciclo segundo
Como vuelven las cifras de una fracción periódica;
Pero sé que una oscura rotación pitagórica
Noche a noche me deja en un lugar del mundo.
Que es de los arrabales. Una esquina remota
Que puede ser del norte, del sur o del oeste,
Pero que tiene siempre una tapia celeste,
Una higuera sombría y una vereda rota.
Ahí está Buenos Aires. El tiempo que a los hombres
Trae el amor o el oro, a mí apenas me deja
Esta rosa apagada, esta vana madeja
De calles que repiten los pretéritos nombres
De mi sangre: Laprida, Cabrera, Soler, Suárez…
Nombres en que retumban (ya secretas) las dianas,
Las repúblicas, los caballos y las mañanas.
Las felices victorias, las muertes militares.
Las plazas agravadas por la noche sin dueño
Son los patios profundos de un árido palacio
Y las calles unánimes que engendran el espacio
Son corredores de vago miedo y de sueño.
Vuelve la noche cóncava que descifró Anaxágoras;
Vuelve a mi carne humana la eternidad constante
Y el recuerdo ¿el proyecto? de un poema incesante:
“Lo supieron los arduos alumnos de Pitágoras…”
Jorge Luis Borges
Compártelo
Por el camino de Swann
“Otras veces, así como Eva nació de una costilla de Adán, una mujer nacía mientras yo estaba durmiendo, de una mala postura de mi cadera. Y siendo criatura hija del placer que y estaba a punto de disfrutar, se me figuraba que era ella la que me lo ofrecía. Mi cuerpo sentía en el de ella su propio calor, iba a buscarlo, y yo me despertaba.
Todo el resto de los mortales se me aparecía como cosa muy borrosa junto a esta mujer, de la que me separara hacía un instante: conservaba aún mi mejilla el calor de su beso y me sentía dolorido por el peso de su cuerpo. Si, como sucedía algunas veces, se me representaba con el semblante de una mujer que yo había conocido en la vida real, yo iba a entregarme con todo mi ser a este único fin: encontrarla; lo mismo que esas personas que salen de viaje para ver con sus propios ojos una ciudad deseada, imaginándose que en una cosa real se puede saborear el encanto de lo soñado. Poco a poco el recuerdo se disipaba; ya estaba olvidada la criatura de mi sueño.”
– Marcel Proust
Exégesis y poesía 